渭南乡镇可约全国空降——多种“可约”概念大解析
视频介绍
判断多项式在有理数域上是否可约有哪些方法
好啦,咱们先来说说多项式可约的问题,别看它听起来挺高大上,但理解起来其实不复杂。比方说,考虑多项式 x^4 - 4,在有理数域上它确实是可约的,尽管它没有有理根。你可能会纳闷,没有理根还可约?没错!这是因为它可以拆成 (x^2 - 2)(x^2 + 2) 两个因式,而这两个因式在有理数域上则都是不可约的。
所以,想判断一个多项式在有理数域上是否可约,可不是单靠找有理根那么简单。咱们还有第二个更靠谱的方法——艾森斯坦判别法!别急,这东西听起来有点吓人,其实是一种相当精确的判定手段,能帮你快速确定大多数多项式的可约性。总之,这两个方法都能用上,真是给了咱们不少方便呢。

什么是弱对角占优矩阵和可约矩阵,它们各自有什么重要性
说矩阵,别害怕,咱们一点点捋明白!先打个比方,弱对角占优矩阵简单说,就是在矩阵里那个“对角线”上的数比同行其他数加起来还要“霸气”一点,但不一定是绝对的霸权。然后要说的就是那种不可约矩阵了,直白点儿讲,就是没法被拆成一堆更小的三角块矩阵的“硬核”矩阵。
-
不可约弱对角占优矩阵:这货可不简单,既满足弱对角占优,又是不可约的,意味着你无法通过简单手段把它分割开。为什么重要?嘿,这类矩阵在数值分析里可是明星,保证了许多计算过程(像谱分解)能妥妥儿地收敛,尤其在解线性方程和找特征值时它们的作用大大的!
-
矩阵的约化:说白了,就是通过置换变换,把矩阵变成分块上三角矩阵。这就像把一大锅杂烩分类摆放,方便你快速搞定。不可约矩阵就相当于那锅杂烩里无法被分成清晰分类的主料。而约化的意义,就是能有效加速对称大型稀疏矩阵的运算,让计算效率一飞冲天。
总得来说,理解这些矩阵的特性,真的是玩转数值分析的一把利器,不信你试试!
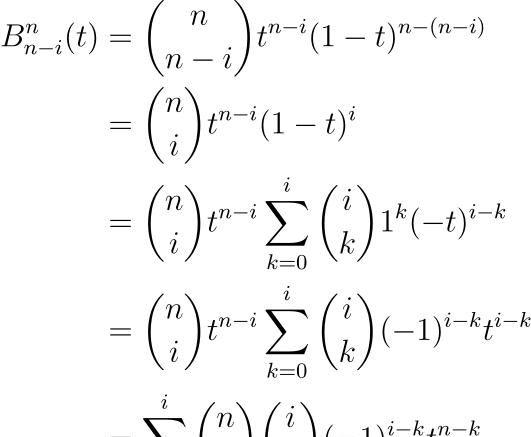
全市可约是什么意思 追女生时究竟什么时候能够约她出来一起吃饭 相关问题解答
先给大家普及个“生活科普”——“全市可约”是什么意思?其实超级简单,就是“全市范围内都能预约”,无论你在哪个角落,都可以顺利约到对应的服务或者资源,挺方便的吧!
在恋爱情场,啥时候能约女生出来吃饭呢?这活儿可是大有讲究:
- 可约的3个信号
- 女生连续三次以上主动延伸话题,比如聊完电影后她会问“你平时还喜欢做什么”,明显想深聊。
- 线下见面时肢体放松,比如并肩走的时候距离小于30厘米,且不躲着你。
-
接受你的小帮助,比方修电脑或者帮拿快递,这说明她愿意和你更亲近。
只要这三个信号里出现两个,你就可以勇敢地邀请她出门啦! -
场合选择的递进
找个舒适不尴尬的地方,不要一上来就太正式或者太吵闹,逐步加深互动,超级OK!
相关问题解答
-
多项式在有理数域上怎么判断是否可约?
哎呀,这个问题其实挺好玩的!简单来说,咱们不能只看有没有有理根,因为某些多项式虽然没有理根,但依然能拆成几个因式。比较靠谱的方法就是用艾森斯坦判别法,它就像专业的侦探,能帮你准确找到那些可约的多项式。总之,找有理根是最快捷的,但不够全面,想稳妥,就用判别法吧! -
为什么不可约弱对角占优矩阵那么重要?
这个矩阵在数值分析里简直是“超级英雄”啊!它不仅稳定,而且保证很多计算(比如求特征值)能顺利收敛,效率倍儿棒。说白了,它让你的数学计算不会陷入死胡同,轻松搞定复杂问题,特别是在工程和科学计算中简直不能缺! -
约化矩阵有什么实用意义吗?
嘿,这个约化过程就是给复杂矩阵“瘦身”和分类,把大块内容分门别类地处理,让计算更快更轻松。特别是在处理超大型、稀疏矩阵时,你懂的,速度和效率都会飞跃提升。就像把乱七八糟的东西放进各个箱子,想拿啥一找就到,超级实用! -
约女生出来吃饭有什么秘诀?
告诉你,别太急躁,先观察她的信号。比如她愿意多跟你聊天,肢体语言放松,还有愿意接受小帮忙,这些都是大大的绿灯!别忘了,场合也很重要,找个舒服又不会尴尬的地方,两个人能聊得开心才是关键。反正听从感觉走,多点真诚,成功率蹭蹭上涨!

评论